Learn
Inequalities
Before we start, make sure we remember these important facts:
- < means less than
- > means greater than
- ≤ means less than or equal to
- ≥ means greater than or equal to
- ≥ means greater than or equal to
- Use an open circle for < or > when graphing
- Use a closed circle for ≤ or ≥ when graphing
Equation vs. Inequality
There is only one difference between an equation and an inequality
An equation has an equal sign: =
An inequality has one of these: <, >, ≤, ≥
Example #1
Open Solve and Graph One-Step Inequalities in One Variable Example #1 in a new tab
Graphing Inequalities
Remember the following when graphing inequalities:
Use an open circle for < or >
Use a closed circle for ≤ or ≥
Example #2
Graph the solution for x < 8.
- Step One: Draw a number line
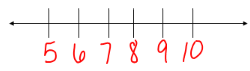
- Step Two: Will you use an open or closed circle?
- open circle
- closed circle
Answer: a. open circle
- Step Three: Determine which way your arrow goes by substituting a number in for the variable to make the statement true. Then, draw the arrow pointing in the correct direction.
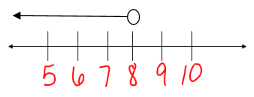
Example #3
Open Solve and Graph One-Step Inequalities in One Variable Example #3 in a new tab
Example #4
Open Solve and Graph One-Step Inequalities in One Variable Example #4 in a new tab
Example #5
Open Solve and Graph Two-Step Inequalities in One Variable Example #5 in a new tab
Example #6
Graph the inequality x < 12.
Open circle or closed circle?
Which direction should the arrow go?
Graph the inequality.
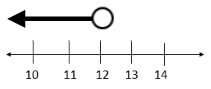
Example #7
Graph the inequality 42 ≥ m.
Open circle or closed circle?
Which direction should the arrow go?
Graph the inequality.
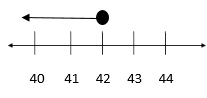
Important Rule: Dividing or Multiplying By a Negative
When you divide or multiply by a negative value, you must flip the inequality sign of your final answer.
This does not apply to adding or subtracting.
Example #8
Solve and graph the inequality −4x ≤ 12.
First, divide both sides by −4 to isolate the variable. Because you are dividing by a negative value, you must remember to flip your sign.
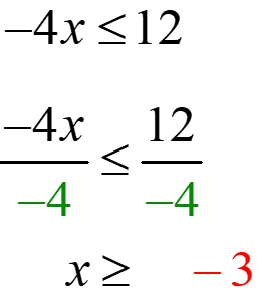
Don't forget to flip the sign because you divided by a negative value.
Graph this inequality.
Answer: 
Graph B is correct. You have a closed point at −3 and all values "greater than or equal to" this point will make the inequality true.
Check your answer using the original inequality. Apply the Symmetric Property and substitute −3 in the original equation.
- −4x = 12
- −4(___blank) = 12
- −4(−3) = 12
- ___blank = 12
- 12 = 12
When simplified, you can determine that your answer does check.
Example #9
Solve and graph the inequality:
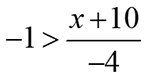
Apply the symmetric property to rewrite the inequality with the variable on the left side.
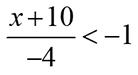
Apply the Multiplication Property and eliminate the denominator by multiplying on both sides. What else is important here? When multiplying by a negative value, the inequality sign must be flipped.
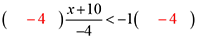
The denominator will be eliminated on the left side, so simplify the right side.
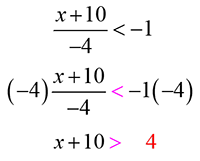
Remember to flip your sign!
Isolate the variable on the left side of the inequality. Apply the Subtraction Property and subtract 10 on both sides of the inequality.
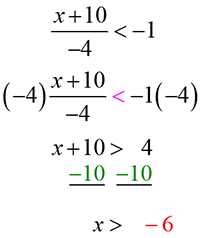
To graph the inequality x > −6, will you have an open or closed point?
- Open Point
- Closed Point
Answer: a. Open Point.
Will you shade your graph to the left or to the right of the point?
- Left
- Right
Answer: b. Right.
Your inequality is x > −6, so you will have an open point and your graph will be shaded to the right.
Choose the correct graph for the inequality x > −6.
Answer: Graph C. 
Check the answer x > −6 using the original inequality.
Apply the substitution property to substitute the answer into the original inequality. Change the inequality sign to an equal sign.
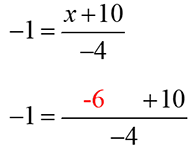
Simplify −6 + 10 in the numerator. Next, you will simplify the fraction.
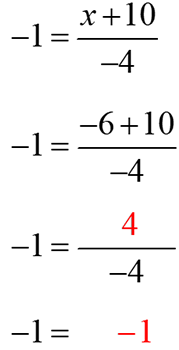
You should find that your answer checks!





