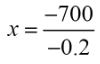Quadratic Function/Applications Resources
Formulas to find the vertex of a parabola:
Definition: Revenue is the income that a company/business receives from its normal business activities. For problems in this lesson, those activities will be the sale of goods - items.
Example Problem # 1
Joe has a taco booth at the state fair. He has found that his daily costs are approximated by the following equation:
C(x) = x2 - 30x + 250
C(x) is the cost in dollars to sell x units of tacos.
The above equation can be used to determine the number of units of tacos he must sell to minimize his cost. The minimum cost can also be found.
Since the equation is a quadratic equation, the vertex formula can be used to determine the number of units of tacos as well as the minimum cost.
To find the minimum amount Joe needs to sell as well as the maximum cost, we will find the vertex using the equation C(x) = x2 - 30x + 250. What is the x-value of the vertex?
x = _?_
Answer: x = 15
To find the minimum amount Joe needs to sell as well as the maximum cost, we will find the vertex using the equation C(x) = x² - 30x + 250. What is the y-value of the vertex?
C(x) = x2 - 30x + 250
C(15) = (15)2 - 30(15) + 250
C(15) = 225 - 450 + 250
C(15) = y =_?_
Answer: y = 25
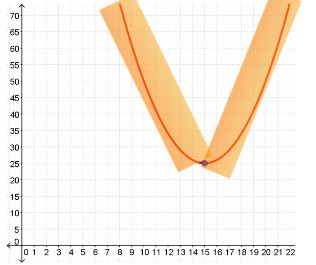
Given the equation C(x) = x2 - 30x + 250, we found the vertex to be at (15, 25). Keep in mind that the amount of money earned depends on the number of tacos.
The vertex tell us this is a minimum point at which Joe will make a profit. Therefore, Joe must sell 15 units of tacos in order to achieve a minimum daily operating cost of $25. In other words, Joe will lose money if he does not sell his minimum of 15 units of tacos.
Still need more explanation? Let's look at this graphically below. We know the vertex is (15, 25) and this is a minimum point.
Anything where the parabola is decreasing is decreasing Joe's profit. Anything at the minimum and increasing on the parabola is where Joe will earn profit.
Example Problem # 2
Let's consider another example. Suppose a model rocket is launched-projected straight upward from a platform 5 feet above the ground. The following formula will give the height h of the rocket after t seconds:
h = - 16t2 + 192t + 5
We want to know two things:
- How long will it take the rocket to reach maximum height?
- What will be the rocket’s maximum height?
The vertex formula for a quadratic equation/function can be used to find the amount of time and the rocket’s maximum height.
Using the equation h = -16t2 + 192t + 5, we need to determine the vertex so we can determine the maximum height of the rocket. What is the x-value of the vertex?
x =_?_
Answer: x = 6
Using the equation h = -16t2 + 192t + 5, we need to determine the vertex so we can determine the maximum height of the rocket. What is the y-value of the vertex?
y = - 16(6)2 + 192(6) + 5
y = -16(36) + 1152 + 5
y = -576 + 1152 + 5
y =_?_
Answer: y = 581
Therefore, if we have the equation h = -16t2 + 192t + 5, then we have our vertex at (6, 581).
This tell us the answer to our two questions:
- It will take the rocket 6 seconds to reach maximum height.
- The maximum height of the rocket after 6 seconds will be 581 feet.
Example Problem # 3
The value of Tom’s stock portfolio is given by the function v(t) = 100 + 78t - 3t2 , where v is the value of the portfolio and t is the time in months.
Using this equation, we want to determine two things:
- How much money did Tom originally invest?
- When will the value of Tom’s portfolio be at a maximum?
To determine the original amount of Tom's investment, we will use the function v(t) = 100 + 78t - 3t2 , we will need to find the value when t = 0. So, we can substitute t = 0 in our original equation.
v(t) = 100 + 78t - 38t2
v(0) = 100 + 78(0) - 38(0)2
v(0) = 100 + 0 - 38(0)
v(0) =_?_
Answer: 100
The next question we were asked to determine was the number of months it would take for Tom's portfolio to reach its maximum. Using the function v(x) = 100 + 78x - 3x2 , we only need to determine the x-value for the vertex.
x =_?_
Answer: x = 13
Using the equation v(x) = 100 + 78x - 3x2, we found the x-value to be x = 13. This represents the number in months it will take for the portfolio to reach its maximum.
The problem only asked for the amount of time that it would take for Tom’s portfolio to reach its maximum. All that needs to be found for this problem is t. It will take 13 months for the investment to reach its maximum.
Example Problem # 4
Find the number of units that a company needs to produce to reach a maximum revenue by using the following revenue equation/function:
R = 700x - 0.1x2
R represents the total revenue (in dollars) and x is the number of units sold.
The vertex formula can be used to determine the total revenue and the number of units that need to be sold.
Using the function R = 700x - 0.1x2, we can determine the coordinate point of the vertex. What is the x-value of the vertex?
x =_?_
Answer: 3500
Using the function R = 700x - 0.1x2, we can determine the coordinate point of the vertex. What is the y-value of the vertex?
R = 700 (3500) - 0.1(3500)2
R = 2,450,000 - 0.1(12,250,00)
R = 2,450,000 - 1,225,00
R =_?_
Answer: 1,225,000
Using the function R = 700x - 0.1x2, we found the vertex to be (3500, 1,225,000).
This means that:
- 3500 units need to be produced for the company to reach its maximum revenue.
- The maximum amount of revenue is $1,225,000.
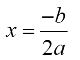
![x = (-[30]/2[1])](../../6_unit/06-03/images/06_03_learn_slide1_equation3.JPG)
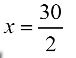
![x = (-[192]/2[-16])](../../6_unit/06-03/images/06_03_learn_slide1_equation5.JPG)
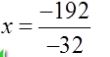
![x = (-[78]/2[-3])](../../6_unit/06-03/images/06_03_learn_slide1_equation7.JPG)
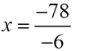
![x = (-[700]/2[-0.1])](../../6_unit/06-03/images/06_03_learn_slide16_equation9.JPG)