Following successful completion of this lesson, students will be able to:

  • Use linear programming procedures to find the maximum or minimum value of an objective function given a set of constraints on the variables of the objective function

The above objectives correspond with the following Alabama Course of Study Objectives: CCRS 4Determine maximum and minimum values of a function using linear programming procedures..

Introduction


Constraints

Decision makers in many fields try to find ways to allocate resources to maximize profits or to minimize costs.

The quantity that is to be maximized or minimized is represented by a function that is called the objective function.

The restrictions that are placed on available resources can be represented by a system of inequalities. This system of inequalities are called the constraints.

The graph of the constraints is called the feasible region. The feasible region is where all of the inequalities overlap. Any point in the feasible region satisfies each of the inequalities.

We are interested only in the vertices of the feasible region, because it has been proven that the maximum or minimum will occur at a vertex.

→


Example

Let's consider the following system of constraints:

  • x + y ≤ 4
  • 2x - y ≤ 2
  • x ≥ 0
  • y ≥ 0

Graph of the constraints x + y < 4, 2x – y < 2, x > 0, y > 0

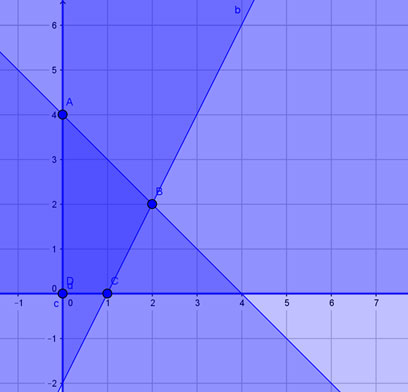
The graph shown above is the graph of the constraints. To determine a maximum or minimum, an objective function is needed. Let's use P = 3x + 2y as our objective function.

Our points are:

  • A (0, 4)
  • B (2, 2)
  • C (1, 0)
  • D (0, 0)

Each of these points contain values for x and y that will be used in the objective function to determine the maximum or minimum. Let's take a look.

A (0, 4): P = 3(0) +2(4) = 0 + 8 = 8
B (2, 2): P = 3(2) + 2(2) = 6 + 4 = 10
C (1, 0): P = 3(1) + 2(0) = 3 + 0 = 3
D (0, 0): P = 3(0) + 2(0) = 0 + 0 = 0

The maximum for this is 10 which occurs when x = 2 and y = 2.

←

 

 

    Next Page