Solving Linear Systems: Graphing
To solve by graphing, you must accurately graph each of the equations in the system and find their point of intersection. Solve the following system by graphing:
y = -2x + 5
x - 3y = 6
First, put both equations in y = mx + b form. The first equation is already in y = mx + b form, so let's start with the second equation.
Solve the second equation for y:
x - 3y = 6
Subtract x from both sides.
- 3y = - x + 6
Divide all terms by -3.
y = (1/3)x - 2
Now the system looks like this. y = -2x + 5 y = 1 x - 2
| y = -2x + 5 | y = (1/3)x - 2 |
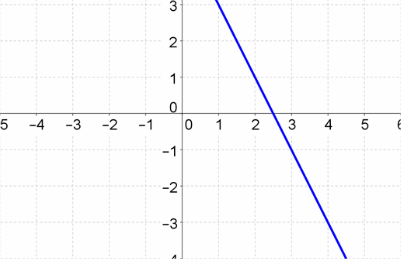 |
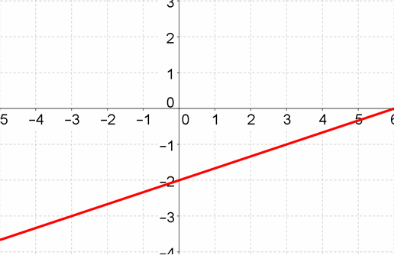 |
Now, look at the two graphs of the two equations when combined.
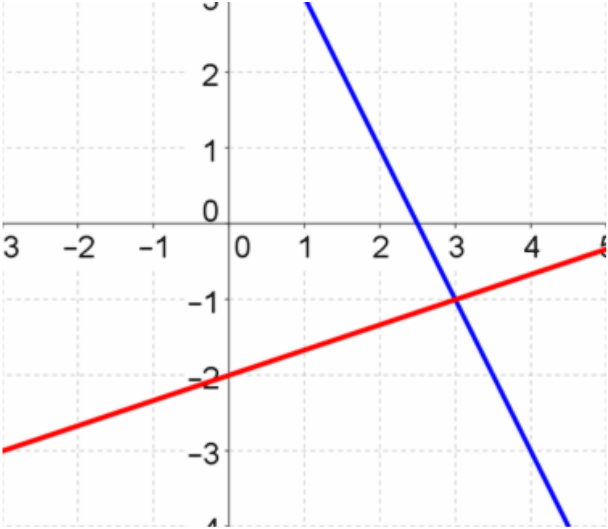
The solution of this system is ( , )
Answer: (3, -1)
Check your solution by substituting into both of the original equations.
y = -2x + 5
-1 = -2(3) + 5
-1 = -6 + 5
-1 = -1
x - 3y = 6
3 - 3(-1) = 6
3 + 3 = 6
6 = 6
Since the ordered pair (3,-1) makes both equations true, it is the solution to the system.