Types of Linear Systems
Systems of linear equations can be classified by the number of solutions.
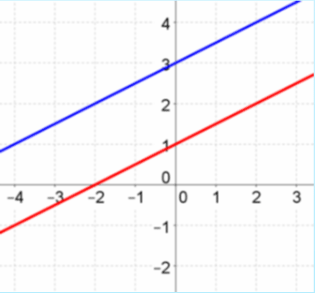
An inconsistent system has no solutions.
- Its graph is the graph of two parallel lines.
- In its equations, the slopes are the same and the y-intercepts are different.
y = ½x + 3
y = ½x + 1
A consistent system has at least one solution. There are 2 types of consistent systems. The first type is an independent system.
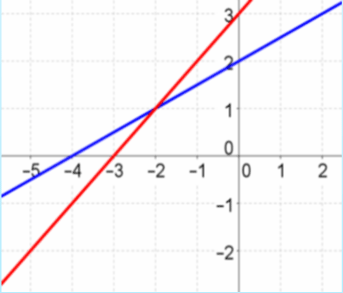
An independent system has exactly one solution.
- Its graph is the graph of 2 lines intersecting in
one point. - In its equations, the slopes are different.
y = ½x + 2
y = x + 3
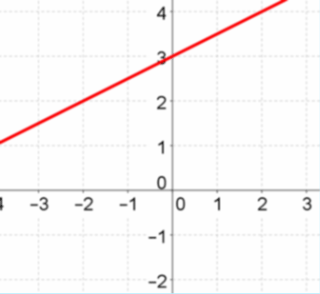
The second type of a consistent system is a dependent system. A dependent system has infinitely many solutions.
- Its graph is the graph of one line lying on top of the other - it looks like a single line.
- In its equations, both the slopes and
y-intercepts are the same.
y = ½x + 2
y = x + 6
As a summary:
| Inconsistent | Consistent and Independent | Consistent and Dependent |
|
|
|
 |
 |
 |
There are 3 ways to solve a system of linear equations:
- Graphing
- Substitution
- Elimination
Next, we will solve systems using these methods.